astar-algorithm

Author Avatar
Euan 1月 04, 2021
  • 在其它设备中阅读本文章

A*算法

算法介筛

A(A-Star)算法是一种启发式搜索方法，目前在网络路由算法、机器人探路、人工智能、游戏设计等方面有着普遍的应用。
　　
A算法一般是以估价函数 的大小来排列待扩展状态的次序，每次选择 f(n) 值最小者进行扩展。

f(n)=g(n)+h(n)

其中g(n) 是初始结点到n结点的实际代价，而h(n)是从n结点点到目的结点的最佳路径的估计代价，且h(n)<=h(n), h(n)为n结点到目的结点的最优路径的代价。

保证找到全局最优解的条件，关键在于估价函数h(n)的选取：

  • 估价值h(n)小于等于n结点到目标结点最优路径的距离实际值，这种情况下，搜索的点数多，搜索范围大，效率低，但能得到全局最优解。
  • 如果估价值h(n)大于实际值, 搜索的点数少，搜索范围小，效率高，但不能保证得到全局最优解。
  • 估价值与实际值越接近，估价函数取得就越好。

自动寻路问题演示

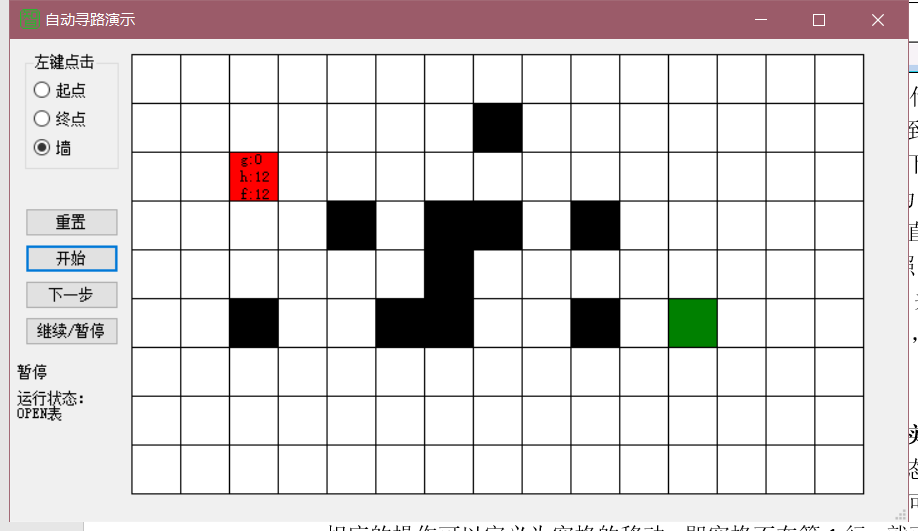
sP1ofx.png

选择好起点、终点、墙后，开始第一步

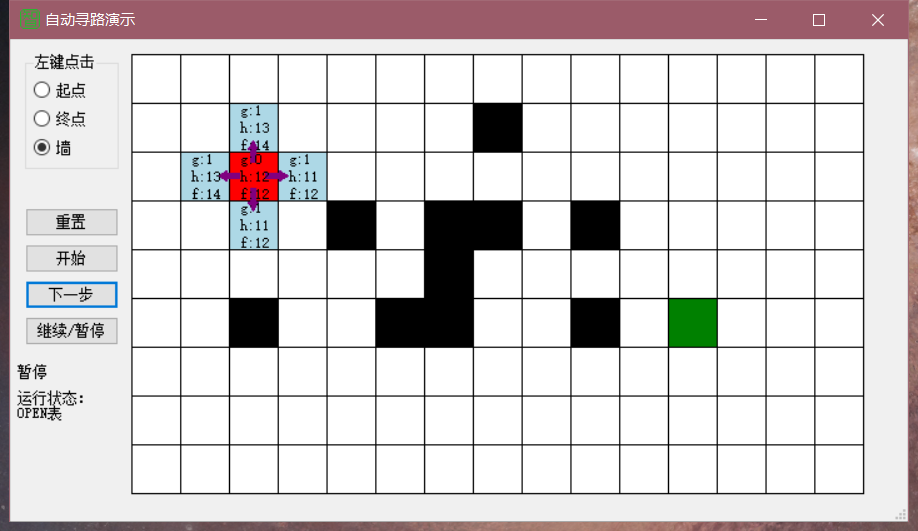
simH7q.png

sim7Bn.png

估计代价h使用的是起点到终点的哈密尔顿距离，即起点到终点的横向和纵向的方格数之和

实际代价g使用的是搜索深度，即搜索步数

此时扩展结点的g值一定相同，而h值则根据每个扩展点的哈密顿距离的不同而不同

扩展点数量:39

实际代价g特点：g每走一步自增1

估计代价h：格子前进的方向h会根据最小的哈密顿距离方向行走，若有墙，则另寻次优最佳路径，到终点时的代价必为0

f到重点时的代价等于实际代价g

8数码问题演示

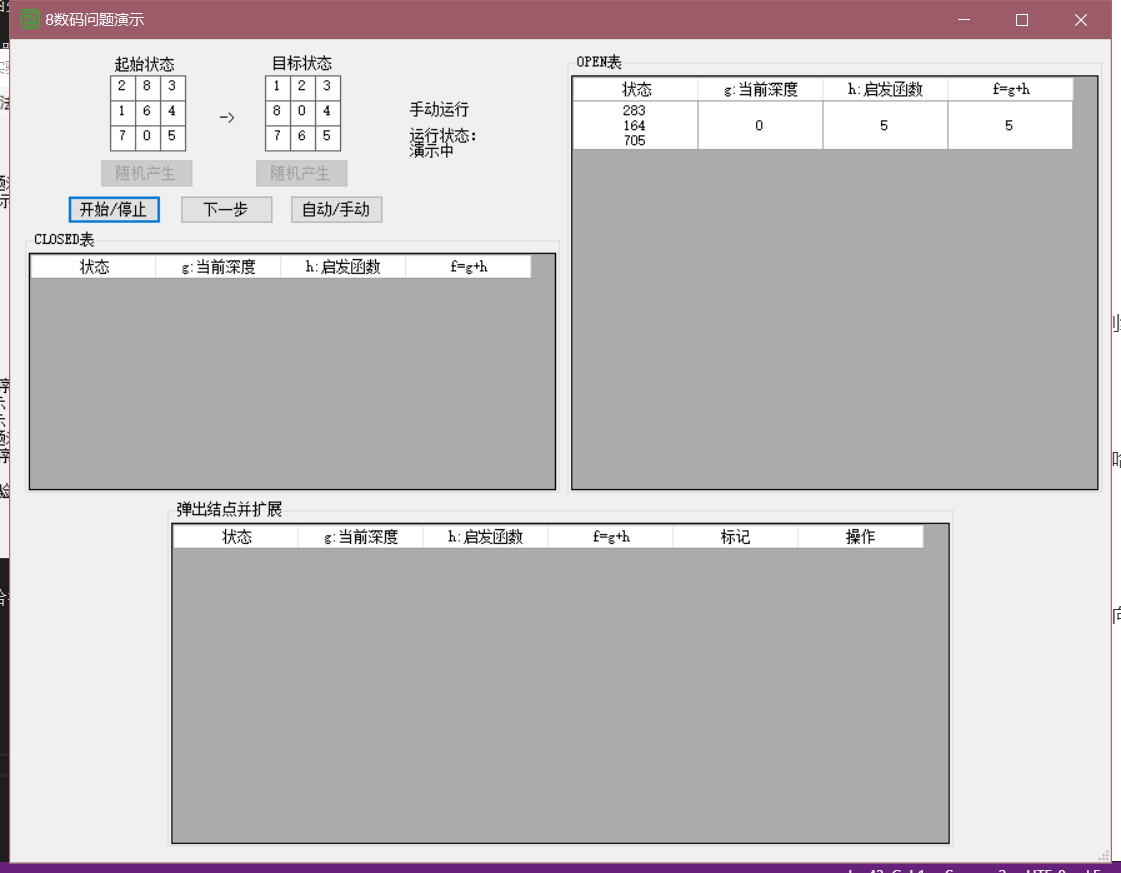
sim5cQ.png

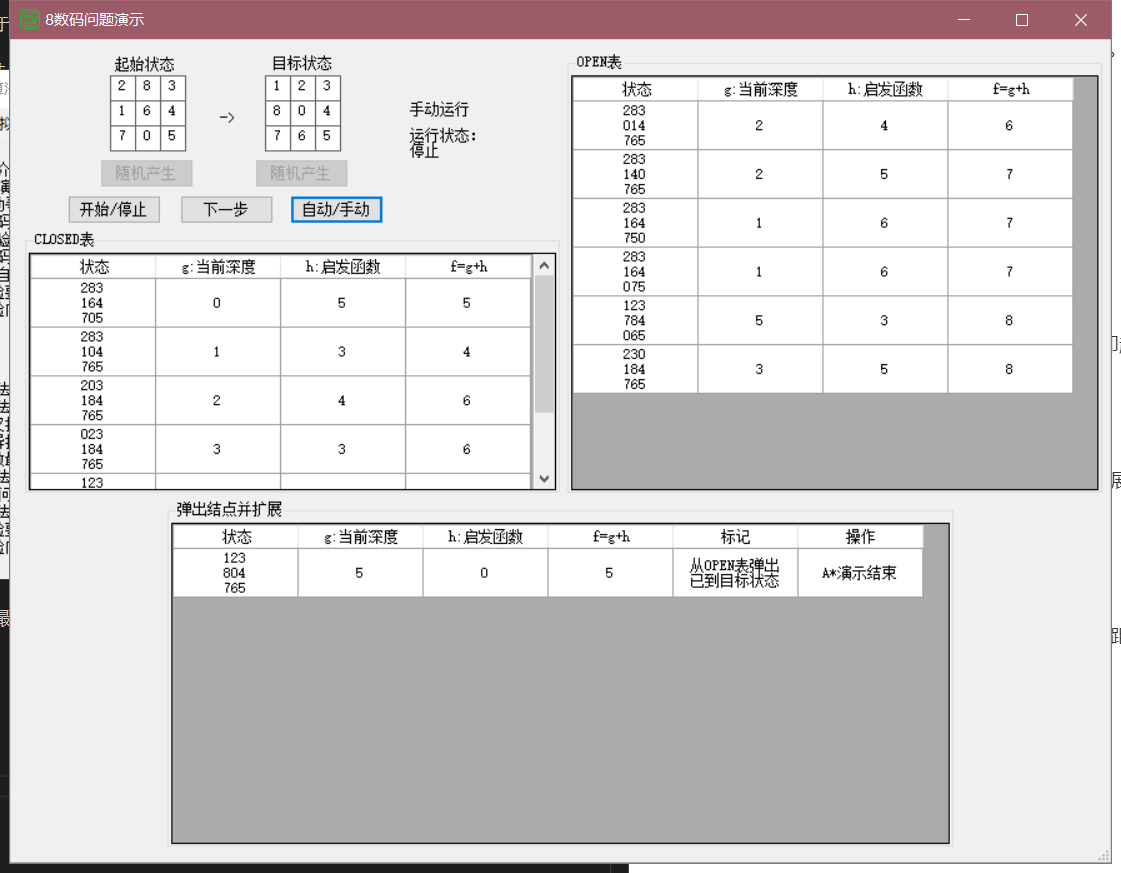
simTns.png

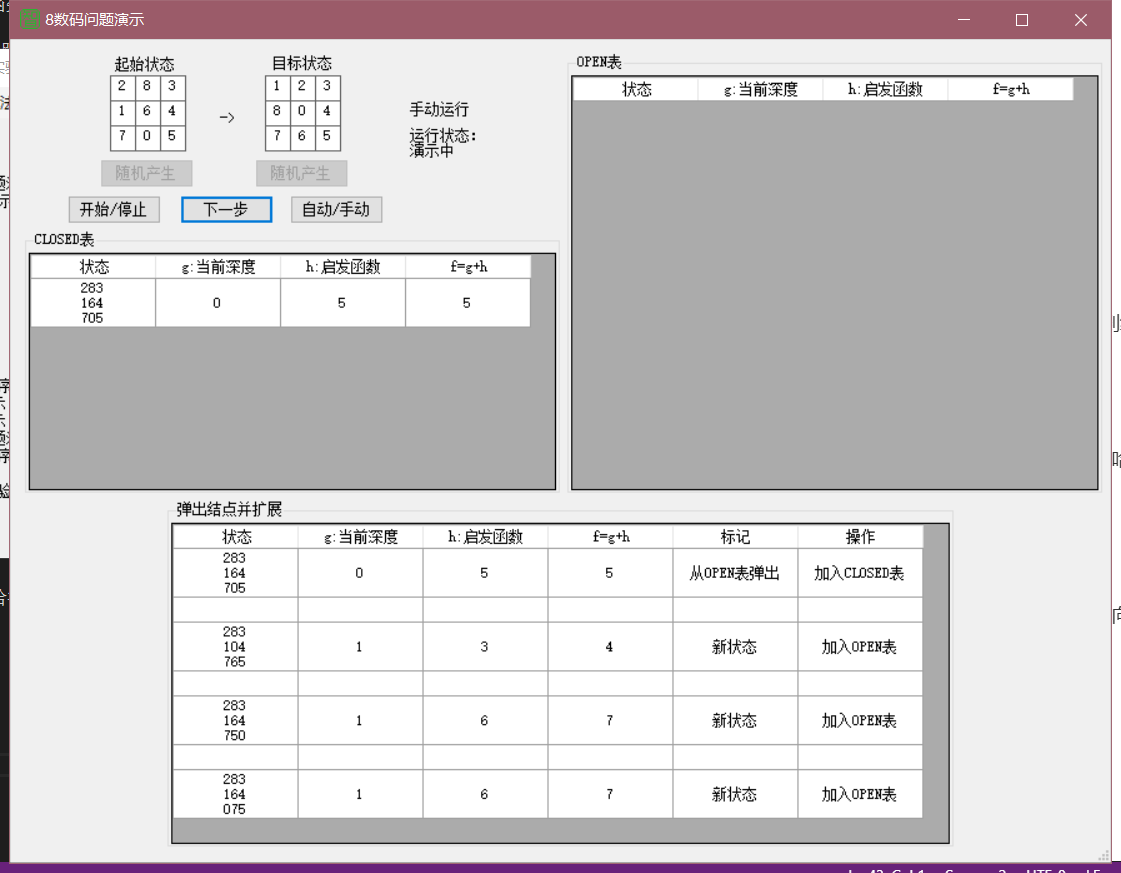
simIXj.png

close、open表均有六个，扩展点一共为12个

实际代价g特点：g每走一步自增1

估计代价h：格子前进的方向h会根据最小的哈密顿距离方向行走，若有墙，则另寻次优最佳路径，到终点时的代价必为0

f到重点时的代价等于实际代价g

8数码问题验证

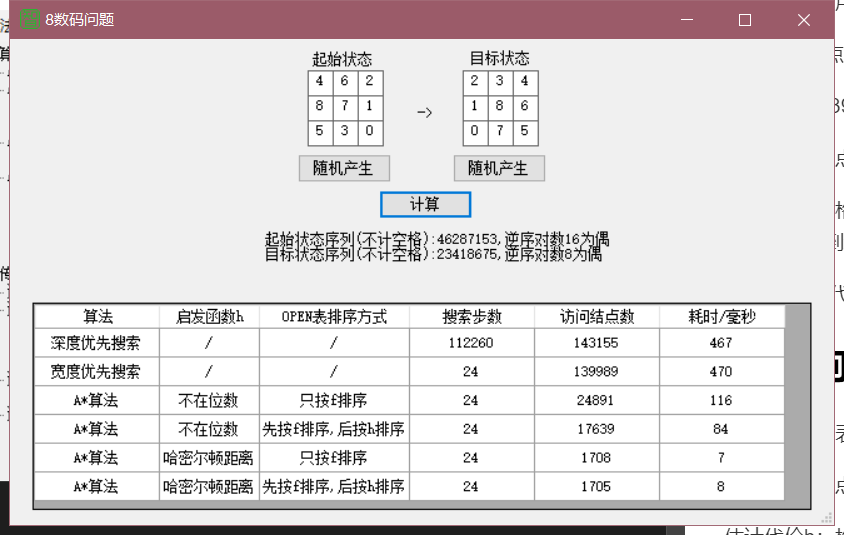
simqA0.png

只有同奇或同偶时才有解

分析为什么A*算法和宽度优先搜索都能找到最优解，即搜索步数都是最少，但它的性能，包括访问结点数和耗时都比宽度优先搜索要少？为什么A*算法采用哈密尔顿距离作为启发函数比不在位数为启发函数的性能要好?

  • 由于8数码问题的树很深，若用深度遍历算法会多余不必要的步骤，比如最优解的下一步用深度遍历来搜索可能会走一个循环，并且深度遍历的搜索思想与广度和A*的扩展思想不搭边，不能用启发性思想，所以难以找到最优解。
  • 而广度优先遍历虽能找到，但也是无目的的找，而A*算法设置了g和h来引导算法更块的找到最优解
  • 关于哈密尔顿和不在位数的区别课程中没有详细讲到这两个算法的区别，网上的资料有限，经过思考后还是不能想出性能不同的根本性原因。
  • 个人觉得哈密尔顿适合多位数的路径查询，而不在位数更倾向与少位的搜索

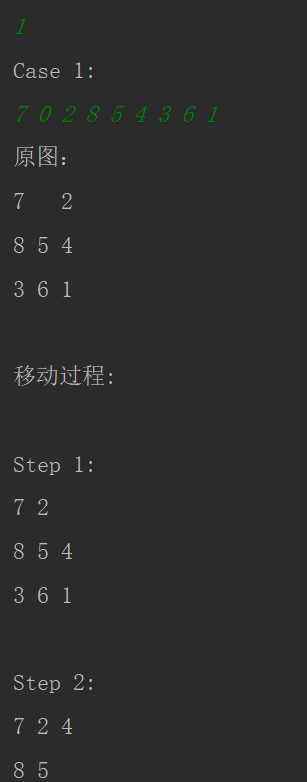
8问题代码实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
//
// Created by ruadhan on 2021/1/4.
//A*算法求解八数码问题

#include<iostream>
#include<map>
#include<queue>
#include<algorithm>
#include<string>
using namespace std;

struct P{
	int d;	//深度g(n)
	int w;	//不在位数h(n)
	int id;	//记录该节点的id，用于输出时找到该节点
	string s;	//状态
	friend bool operator <(const P &a,const P &b){//按f(n)=g(n)+h(n)大小排序
		return a.d+a.w>b.d+b.w;  //最大堆
	}
}p;
const int N=3;	//棋盘大小
//const string t="123456780";	//目标状态
const string t="123804765";
string stack[1000000];		//记录搜索中的节点
string record[1000000];		//从起点开始记录解路径
int father[10000000];		//记录该节点的父节点
int top=0;					//stack的指针
priority_queue<P> pq;		//open表
map<string,bool> mp;		//记录该状态是否已经访问过：1访问过，0没有

int calw(string s)//计算该状态的不在位数h(n)
{
	int re=0;
	for(int i=0;i<9;i++) if(s[i]!=t[i]) re++;
	return re;
}
int solve()	//搜索过程
{
	P cur;
	while(!pq.empty()){
		cur=pq.top(); //open表
		pq.pop();
		if(cur.s==t) return cur.id;	//达到目标状态，返回当前节点的id
		int x,y;
		int ops=0;
		while(cur.s[ops]!='0') ops++;
		x=ops/3,y=ops%3;  //空格所在位置
		int r=cur.id;
		if(x>0){          //空格向上移
			p.s=cur.s;
			swap(p.s[ops],p.s[ops-3]);
			if(!mp[p.s]){
				p.d=cur.d+1,p.w=calw(p.s),p.id=top+1;
				pq.push(p);
				stack[++top]=p.s;
				father[top]=r;
				mp[p.s]=1;
			}
		}
		if(x<2){    //空格向下移
			p.s=cur.s;
			swap(p.s[ops],p.s[ops+3]);
			if(!mp[p.s]){
				p.d=cur.d+1,p.w=calw(p.s),p.id=top+1;
				pq.push(p);
				stack[++top]=p.s;
				father[top]=r;
				mp[p.s]=1;
			}
		}
		if(y>0){    //空格向左移
			p.s=cur.s;
			swap(p.s[ops],p.s[ops-1]);
			if(!mp[p.s]){
				p.d=cur.d+1,p.w=calw(p.s),p.id=top+1;
				pq.push(p);
				stack[++top]=p.s;
				father[top]=r;
				mp[p.s]=1;
			}
		}
		if(y<2){   //空格向右移
			p.s=cur.s;
			swap(p.s[ops],p.s[ops+1]);
			if(!mp[p.s]){
				p.d=cur.d+1,p.w=calw(p.s),p.id=top+1;
				pq.push(p);
				stack[++top]=p.s;
				father[top]=r;
				mp[p.s]=1;
			}
		}
	}
	return -1;	//搜索失败
}

void print(int x)////从record表中输出当前搜索的节点
{
	int k=0;
	for(int i=0;i<N;i++){
		for(int j=0;j<N;j++){
			if(record[x][k]=='0')
				printf("  ");
			else printf("%c ",record[x][k]);
			k++;
		}
		printf("\n");
	}
	printf("\n");
}
int main()
{
//	freopen("a.txt","r",stdin);
	int tt;	//测试的组数
	cin>>tt;
	for(int k=1;k<=tt;k++){
		cout<<"Case "<<k<<":\n";
		int i,j;
		char a;
		p.s="";
		for(i=0;i<N;i++){
			for(j=0;j<N;j++){
				cin>>a;  //输入0～8数码
				p.s+=a;
			}
		}
		p.d=0,p.w=calw(p.s),p.id=0;
		father[0]=-1;
		mp[p.s]=1;
		stack[0]=p.s;
		pq.push(p);	//往open表中加入初始状态节点
		int id=solve();//调用搜索过程
		if(id==-1){
			cout<<"无解！\n";
		}else{
			int c=-1;
			while(id>=0){	//把stack中存的节点按次序放入到record中
				record[++c]=stack[id];
				id=father[id];
			}
			cout<<"原图："<<endl;
			print(c); //输出初始节点
			cout<<"移动过程: \n\n";
			for(i=c-1;i>=0;i--){
				cout<<"Step "<<c-i<<":\n";//输出当前搜索步骤
				print(i);//输出当前搜索的节点
			}
			cout<<"移动结束！\n";
		}
		mp.clear();
		while(!pq.empty()) pq.pop();
		top=0;
		cout<<endl;
	}
	system("pause\n");
	return 0;
}

si3lLD.png

本文使用 CC BY-NC-SA 3.0 中国大陆 协议许可
具体请参见 知识共享协议
本文链接：https://zyhang8.github.io/2021/01/04/astar-algorithm/