频域图像处理

Author Avatar
Euan 11月 24, 2019
  • 在其它设备中阅读本文章

频域图像处理

实验目的

  1. 掌握图像快速傅里叶变换及其实现
  2. 掌握图像二维频谱的分布特点

实验原理

图像的快速傅里叶变换

傅里叶变换频谱图像

实验内容或步骤

  • 对一张图像进行平移，显示原始图像和处理后的图像；
  • 分别对两幅图像进行傅里叶变换，显示变换后的结果，分析原图傅里叶频谱与平移后图像频谱的对应关系；
  • 对rectangular.jpg及其旋转图rectangular-rotation.jpg分别进行傅里叶变换，显示变换后的结果，分析原图傅里叶频谱与旋转后图像频谱的对应关系。

参考

注意几个图像傅里叶变换的步骤：

  1. 需要先获取最佳DFT变换的大小（cv.getOptimalDFTSize），然后以这个大小对原图进行扩充( padding，cv.copyMakeBorder)
  2. 需要DFT变换后的矩阵进行分解（cv.split），从中提取谱分量（cv.magnitude）
  3. 如果谱分量行列为奇数，需要对其进行裁剪成偶数（cv.Rect）
  4. 如果谱分量太大，需要对其进行对数变换（log），以便更好的显示
  5. 将傅里叶变换后图像的原点调整到中心

实验报告

  • 描述实验的基本原理和步骤
  • 用数据和图片给出各个步骤中取得的实验结果 ，包括原始图像及其处理后的图像，并进行必要的讨论
  • 完整的源代码

图像平移

代码流程如下：

读取图像→显示原图像→调用自定义的函数translateTransform，作平移后图像大小不变的平移处理并显示处理结果→调用自定义的函数translateTransformSize，作平移后图像大小变化的平移处理并显示处理结果。

dst_window显示的是平移时图像尺寸不变的平移结果，可以看见，损失了部分原图；而dst_wind

傅里叶变换，分析原图傅里叶频谱与平移后图像频谱的对应关系

傅立叶变换的步骤

1．需要先获取最佳DFT变换的大小（cv.getOptimalDFTSize），然后以这个大小对原图进行扩充( padding，cv.copyMakeBorder)
2．需要DFT变换后的矩阵进行分解（cv.split），从中提取谱分量（cv.magnitude）
3．如果谱分量行列为奇数，需要对其进行裁剪成偶数（cv.Rect）
4．如果谱分量太大，需要对其进行对数变换（log），以便更好的显示
5．将傅里叶变换后图像的原点调整到中心

什么是DFT，和傅立叶变换有什么联系

根据信号的不同类型，可以把傅立叶变换分为四类：

1) 非周期性连续信号： 傅立叶变换(Fourier Transform，FT)

2) 周期性连续信号： 傅立叶级数(Fourier Series，FS)

3) 非周期性离散信号： 离散时域傅立叶变换(Discrete Time Fourier Transform ,DTFT)

4)周期性离散信号： 离散傅立叶变换(Discrete Fourier Series，DFS)

3

根据时域与频域的对应关系，我们可以知道，周期<—->离散，是一对对偶关系，即周期信号的傅里叶变换一定是离散的，离散信号的傅里叶变换一定是周期的，反之也成立。

所以针对上述四种傅里叶变换，我们知道，FT的结果具有连续非周期性质，FS的结果具有离散非周期性质，DTFT结果具有连续周期性质，DFT结果具有离散周期性质。

非周期连续信号的傅里叶变换(FT)为：

𝐹(𝜔)=∫−∞∞𝑥(𝑡)𝑒−𝑖𝜔𝑡𝑑𝑡

非周期离散序列的傅里叶变换(DTFT)为：

𝐹(𝜔)=∑𝑛=−∞∞𝑥(𝑛)𝑒−𝑖𝜔𝑛𝑇𝑠

周期连续信号的傅里叶变换(FS)为：

𝐹(𝜔𝑘)=1𝑇∫0𝑇𝑥(𝑡)𝑒−𝑖𝜔𝑘𝑡𝑑𝑡=1𝑇∫0𝑇𝑥(𝑡)𝑒−𝑖2𝜋𝑘𝑡/𝑇𝑑𝑡

周期离散信号的傅里叶变换(DFS)为：

𝐹(𝜔𝑘)=∑𝑛=0𝑁−1𝑥(𝑛)𝑒−𝑖𝜔𝑘𝑛=∑𝑛=0𝑁−1𝑥(𝑛)𝑒−𝑖2𝜋𝑘𝑁𝑛

假定x(n)为Ts区域上x(t)的均值，且Ts（抽样间隔）足够小，如下图所示：

2

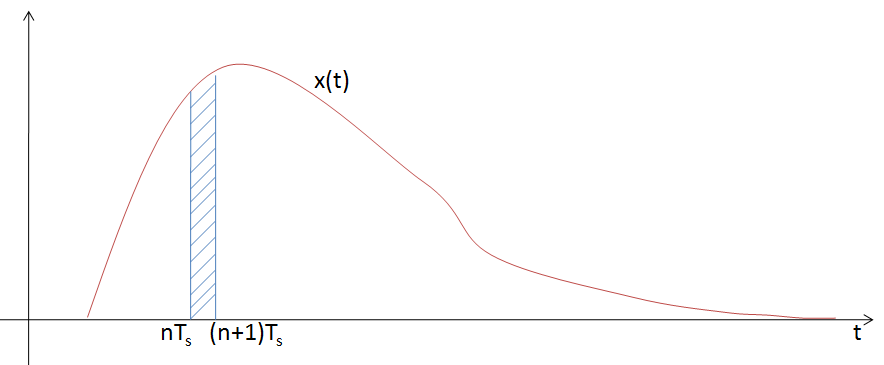
则有

𝐹𝐹𝑇(𝜔)=∫−∞∞𝑥(𝑡)𝑒𝑖𝜔𝑡𝑑𝑡=∑𝑛=−∞∞∫(𝑛+1)𝑇𝑠𝑛𝑇𝑠𝑥(𝑡)𝑒𝑖𝜔𝑡𝑑𝑡=𝑇𝑠∑𝑛=−∞∞𝑥(𝑛)𝑒𝑖𝜔𝑛𝑇𝑠=𝑇𝑠𝐹𝐷𝑇𝐹𝑇(𝜔)

其中

𝑥(𝑛)=1𝑇𝑠∫(𝑛+1)𝑇𝑠𝑛𝑇𝑠𝑥(𝑡)𝑑𝑡

所以非周期连续信号与非周期离散信号之间频谱关系为：

FFT(ω)=Ts·FDTFT(ω) （ω<2πfs）

同样可以推导周期连续信号与周期离散信号之间频谱关系为：

FFS(ωk)=Ts/T·FDFS(ωk)=1/N·FDFS(ωk) （k<N）

上述等式所加的限定是由于离散信号的频谱具有周期性，等价于原连续信号频谱以fs为周期进行平移。这是由于离散信号的傅里叶变换的核函数具有周期性,例如DTFT的核函数为𝑒−𝑖𝜔𝑛𝑇𝑠，当ω增加2πfs时，其值仍然不变。

假若连续信号为一个波包，最高频率为fH,只在有限时间内幅值不为0，则连续信号按周期T延拓后周期信号的傅里叶级数是原连续信号的频域抽样，抽样周期为1/T，其中T为周期信号的周期。公式表示为：

FFS(ωk)=1/T·FFT(ω=ωk)

上述四种傅里叶变换的关系由下图可以对比看出：

1

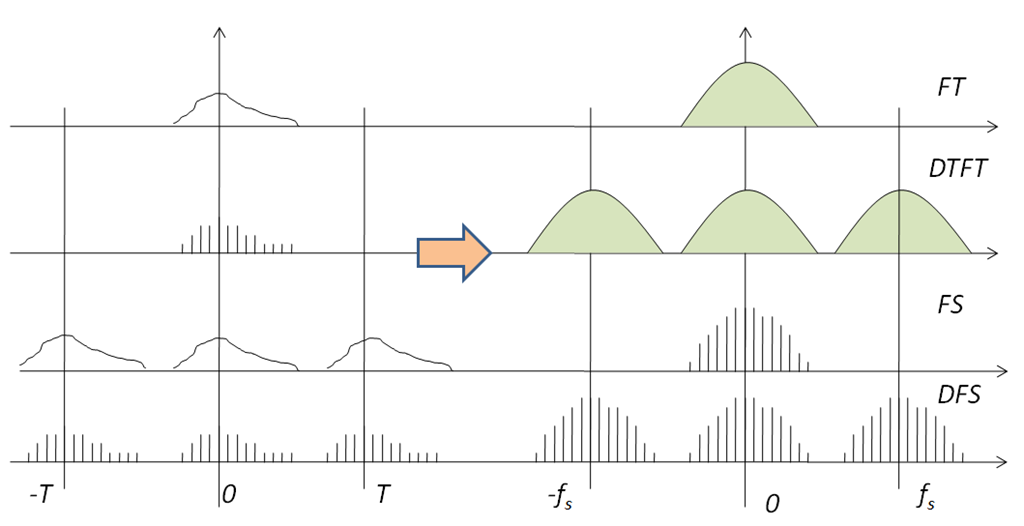
上图中，离散信号的采样周期fs>2fH；FS变换的频谱分辨率为1/T.

在实际使用用计算机处理数据时，要求数据都是有限长度，而上述四种傅立叶变换都是针对无穷长度的信号。

针对有限长度的离散信号，定义了DFT：设x(n)是一个长度为N的有限长序列，则定义x(n)的N点离散傅里叶变换为：

𝑋(𝑘)=𝐷𝐹𝑇[𝑥(𝑛)]=∑𝑛=0𝑁−1𝑥(𝑛)𝑊𝑘𝑛𝑁, k = 0, 1, …, N - 1

其中WN=exp(-j2π/N).

MOhSsI.png

三张图片分别为平移大小不变，平移大小变化，原图，第一张图片把窗口和图片同时增大相应的图片变量，第一张图片只把图片平移导致部分缺失

void dft(InputArray src, OutputArray dst, int flags=0, int nonzeroRows=0);

参数解释：

  • InputArray src: 输入图像，可以是实数或虚数
  • OutputArray dst: 输出图像，其大小和类型取决于第三个参数flags
  • int flags = 0: 转换的标识符，有默认值0.其可取的值如下所示：
  • DFT_INVERSE: 用一维或二维逆变换取代默认的正向变换
  • DFT_SCALE: 缩放比例标识符，根据数据元素个数平均求出其缩放结果，如有N个元素，则输出结果以1/N缩放输出，常与DFT_INVERSE搭配使用。
  • DFT_ROWS: 对输入矩阵的每行进行正向或反向的傅里叶变换；此标识符可在处理多种适量的的时候用于减小资源的开销，这些处理常常是三维或高维变换等复杂操作。
  • DFT_COMPLEX_OUTPUT: 对一维或二维的实数数组进行正向变换，这样的结果虽然是复数阵列，但拥有复数的共轭对称性（CCS），可以以一个和原数组尺寸大小相同的实数数组进行填充，这是最快的选择也是函数默认的方法。你可能想要得到一个全尺寸的复数数组（像简单光谱分析等等），通过设置标志位可以使函数生成一个全尺寸的复数输出数组。
  • DFT_REAL_OUTPUT: 对一维二维复数数组进行逆向变换，这样的结果通常是一个尺寸相同的复数矩阵，但是如果输入矩阵有复数的共轭对称性（比如是一个带有DFT_COMPLEX_OUTPUT标识符的正变换结果），便会输出实数矩阵。
  • int nonzeroRows = 0: 当这个参数不为0，函数会假设只有输入数组（没有设置DFT_INVERSE）的第一行或第一个输出数组（设置了DFT_INVERSE）包含非零值。这样的话函数就可以对其他的行进行更高效的处理节省一些时间，这项技术尤其是在采用DFT计算矩阵卷积时非常有效。

MOfl2d.png

从原图傅里叶频谱与平移后图像频谱可以看出，平移后四条线不会特别的明显，原点也不会很明显

对rectangular.jpg及其旋转图rectangular-rotation.jpg分别进行傅里叶变换

MOfQ8H.png

旋转前的图片频谱分布为十字架型，旋转后的图片的频谱与图片旋转的角度相似，但显然旋转后的频谱有些地方模糊，并且有很多噪点，个人觉得频谱还跟图片的形状有关，如果该图片包括白色的部分也一块旋转，那旋转后就不会那么模糊了

源代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
#include <opencv2/opencv.hpp>
#include <iostream>

using namespace std;
using namespace cv;

void translateTransform(cv::Mat const& src, cv::Mat& dst, int dx, int dy)
{
	CV_Assert(src.depth() == CV_8U);
	const int rows = src.rows;
	const int cols = src.cols;
	dst.create(rows, cols, src.type());
	Vec3b* p;
	for (int i = 0; i < rows; i++)
	{
		p = dst.ptr<Vec3b>(i);
		for (int j = 0; j < cols; j++)
		{
			//平移后坐标映射到原图像  
			int x = j - dx;
			int y = i - dy;
			//保证映射后的坐标在原图像范围内  
			if (x >= 0 && y >= 0 && x < cols && y < rows)
				p[j] = src.ptr<Vec3b>(y)[x];
		}
	}
}
//平移后大小变化  
void translateTransformSize(cv::Mat const& src, cv::Mat& dst, int dx, int dy)
{
	CV_Assert(src.depth() == CV_8U);
	const int rows = src.rows + abs(dy); //输出图像的大小  
	const int cols = src.cols + abs(dx);
	dst.create(rows, cols, src.type());
	Vec3b* p;
	for (int i = 0; i < rows; i++)
	{
		p = dst.ptr<Vec3b>(i);
		for (int j = 0; j < cols; j++)
		{
			int x = j - dx;
			int y = i - dy;
			if (x >= 0 && y >= 0 && x < src.cols && y < src.rows)
				p[j] = src.ptr<Vec3b>(y)[x];
		}
	}
}

Mat my_f(Mat& mImage) {


	int m = getOptimalDFTSize(mImage.rows);//获取最佳DFT变换的大小
	int n = getOptimalDFTSize(mImage.cols);
	copyMakeBorder(mImage, mImage, 0, m - mImage.rows, 0, n - mImage.cols, BORDER_CONSTANT, Scalar(0));//扩充


	Mat mFourier(mImage.rows + m, mImage.cols + n, CV_32FC2, Scalar(0, 0));
	Mat mForFourier[] = { Mat_<float>(mImage), Mat::zeros(mImage.size(), CV_32F) };
	Mat mSrc;
	merge(mForFourier, 2, mSrc);//合并
	dft(mSrc, mFourier);//傅里叶

	vector<Mat> channels;
	split(mFourier, channels);//矩阵分解
	Mat mRe = channels[0];
	Mat mIm = channels[1];

	Mat mAmplitude;
	magnitude(mRe, mIm, mAmplitude);//提取谱分量

	mAmplitude += Scalar(1);
	log(mAmplitude, mAmplitude);//进行对数变换

	//将傅里叶变换后图像的原点调整到中心
	normalize(mAmplitude, mAmplitude, 0, 255, NORM_MINMAX);
	//如果谱分量行列为奇数，需要对其进行裁剪成偶数
	Mat mResult(mImage.rows, mImage.cols, CV_8UC1, Scalar(0));
	for (int i = 0; i < mImage.rows; i++)
	{
		uchar* pResult = mResult.ptr<uchar>(i);
		float* pAmplitude = mAmplitude.ptr<float>(i);
		for (int j = 0; j < mImage.cols; j++)
		{
			pResult[j] = (uchar)pAmplitude[j];
		}
	}

	Mat mQuadrant1 = mResult(Rect(mResult.cols / 2, 0, mResult.cols / 2, mResult.rows / 2));
	Mat mQuadrant2 = mResult(Rect(0, 0, mResult.cols / 2, mResult.rows / 2));
	Mat mQuadrant3 = mResult(Rect(0, mResult.rows / 2, mResult.cols / 2, mResult.rows / 2));
	Mat mQuadrant4 = mResult(Rect(mResult.cols / 2, mResult.rows / 2, mResult.cols / 2, mResult.rows / 2));

	Mat mChange1 = mQuadrant1.clone();
	//mQuadrant1 = mQuadrant3.clone();
	//mQuadrant3 = mChange1.clone();
	mQuadrant3.copyTo(mQuadrant1);
	mChange1.copyTo(mQuadrant3);

	Mat mChange2 = mQuadrant2.clone();
	//mQuadrant2 = mQuadrant4.clone();
	//mQuadrant4 = mChange2.clone();
	mQuadrant4.copyTo(mQuadrant2);
	mChange2.copyTo(mQuadrant4);
	return mResult;
}
int main()
{
	Mat mImage = imread("lena_gray.png", 0);
	Mat mImage1 = imread("dst1.png", 0);
	if (mImage.data == 0)
	{
		cerr << "Image reading error" << endl;
		system("pause");
		return -1;
	}

	namedWindow("original", WINDOW_NORMAL);
	imshow("original", mImage);
	namedWindow("original1", WINDOW_NORMAL);
	imshow("original1", mImage1);
	/*
	Mat dst, dst1;
	translateTransform(mImage, dst, 50, 50);
	namedWindow("dst_window");
	imshow("dst_window", dst);
	imwrite("dst.png", dst);
	translateTransformSize(mImage, dst1, 50, 50);
	namedWindow("dst_window1");
	imshow("dst_window1", dst1);
	imwrite("dst1.png", dst1);
	*/
	
	Mat mresult,mresult1;
	mresult = my_f(mImage);
	mresult1 = my_f(mImage1);
	namedWindow("Fourier1", WINDOW_NORMAL);
	imshow("Fourier1", mresult);
	namedWindow("Fourier", WINDOW_NORMAL);
	imshow("Fourier", mresult1);

	
	Mat rImage = imread("rectangular.jpg", 0);
	Mat rrImage = imread("rectangular-rotation.jpg", 0);
	namedWindow("roriginal", WINDOW_NORMAL);
	imshow("roriginal", rImage);
	namedWindow("rroriginal", WINDOW_NORMAL);
	imshow("rroriginal", rrImage);
	Mat rresult, rrresult;
	rresult = my_f(rImage);
	rrresult = my_f(rrImage);
	namedWindow("rFourier", WINDOW_NORMAL);
	imshow("rFourier", rresult);
	namedWindow("rrFourier", WINDOW_NORMAL);
	imshow("rrFourier", rrresult);


	waitKey();
	destroyAllWindows();
	return 0;
}

本文使用 CC BY-NC-SA 3.0 中国大陆 协议许可
具体请参见 知识共享协议
本文链接：https://zyhang8.github.io/2019/11/24/cv-exp5/