多种密钥面临的的数学难题
多种密钥面临的的数学难题
Diffie-Hellman密钥协商算法
概述
Diffie-Hellman密钥协商算法主要解决秘钥配送问题,本身并非用来加密用的;该算法其背后有对应数学理论做支撑,简单来讲就是构造一个复杂的计算难题,使得对该问题的求解在现实的时间内无法快速有效的求解。
解决思路
为了解决第一个问题,原文提出两种方法:公钥加密系统(public key cryptosystem)和秘钥分发系统(public key distribution system)。对于公钥加密系统,原文只是勾画了一种比较抽象的公钥加密系统的概念模型,重点是加解密采用不同的秘钥,并总结了该系统应该满足的一些特性,相当于是一种思想实验,并没有给出具体的算法实现途径,但这在当时应该来说已经足够吸引人。后来RSA三人组(Ron Rivest、Adi Shamir 和 Leonard Adleman)受此启发,经过许多轮失败的尝试后,于第二年在论文A Method for Obtaining Digital Signatures and Public-Key Cryptosystems中提出了切实可行且很具体的公钥加密算法–RSA公钥加密算法。而对于秘钥分发系统,就是本文的DH秘钥协商算法。
为了解决第二个问题,原文通过单向函数(one-way function)来解决,这就是单向认证的问题。另外作者还讨论了这些密码学问题之间的关联性以及如何相互转化。比如一个安全的密码系统(可以防御明文攻击)可以用来生成一个的单向函数、公钥加密系统可以用来作为单向认证、陷门密码系统可以用来生成一个公钥加密系统。数学难题的计算复杂度被当成一种保障密码学安全问题的有效工具被利用起来,这一重要思想贯穿现代密码学的许多加密算法。
存在的问题
是否DH秘钥协商算法就一定安全呢?应该说也不是,因为存在一种伪装者攻击(或者称为中间人攻击)能够对这种秘钥协商算法构成威胁。
假设秘钥协商过程中,在Alice和Bob中间有一个称为Mallory的主动攻击者,他能够截获Alice和Bob的消息并伪造假消息,考虑如下情况。
1)Alice和Bob已经共享一个素数𝑝及其该素数𝑝的本原根𝑔,当然Mallory监听到报文也得知了这两个消息。
2)此时Alice计算𝑌𝑎=𝑔𝐴𝑚𝑜𝑑𝑝,然而在将𝑌𝑎发送给Bob的过程中被Mallory拦截,Mallory自己选定一个随机数𝑆,计算𝑌𝑠𝑏=𝑔𝑆𝑚𝑜𝑑𝑝,然后将𝑌𝑠𝑏发送给了Bob。
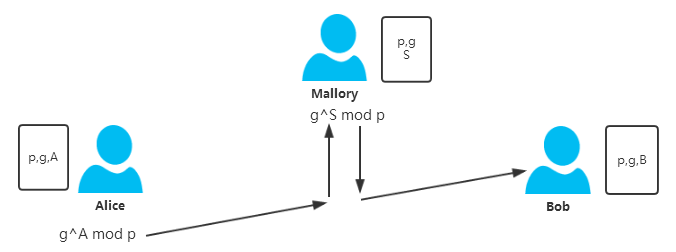
3)同时Bob计算𝑌𝑏=𝑔𝐵𝑚𝑜𝑑𝑝,然而在将𝑌𝑏发送给Alice的过程中被Mallory拦截,Mallory自己选定一个随机数𝑇,计算𝑌𝑡𝑎=𝑔𝑇𝑚𝑜𝑑𝑝,然后将𝑌𝑡𝑎发送给了Alice。
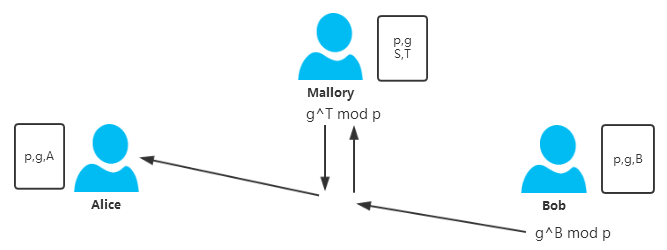
由于通讯消息被替换,Alice计算出的秘钥实际上是Alice和Mallory之间协商秘钥:𝐾𝑎𝑚=𝑔𝐴×𝑇𝑚𝑜𝑑𝑝;Bob计算出的秘钥实际上是Bob与Mallory之间协商的秘钥:𝐾𝑏𝑚=𝑔𝐵×𝑆𝑚𝑜𝑑𝑝。如果之后Alice和Bob用他们计算出的秘钥加密任何信
ECC椭圆加密算法
定义
椭圆加密算法(ECC)是一种公钥加密体制,最初由Koblitz和Miller两人于1985年提出,其数学基础是利用椭圆曲线上的有理点构成Abel加法群上椭圆离散对数的计算困难性。
难题
ECC是建立在基于椭圆曲线的离散对数问题上的密码体制,给定椭圆曲线上的一个点G,并选取一个整数k,求解K=kG很容易(注意根据kG求解出来的K也是椭圆曲线上的一个点);反过来,在椭圆曲线上给定两个点K和G,若使K=kG,求整数k是一个难题。ECC就是建立在此数学难题之上,这一数学难题称为椭圆曲线离散对数问题。其中椭圆曲线上的点K则为公钥(注意公钥K不是一个整数而是一个椭圆曲线点,这个点在OpenSSL里面是用结构体EC_Point来表示的,为了加深理解,建议自行下载OpenSSL进行查看学习),整数k则为私钥(实际上是一个大整数)。
不知我说明白了没有,这是网上的一位网友总结的,供参考:
考虑如下等式:K=kG [其中 K,G为Ep(a,b)上的点,k为小于n(n是点G的阶)的整数],不难发现,给定k和G,根据加法法则,计算K很容易;但给定K和G,求k就相对困难了。这就是椭圆曲线加密算法采用的难题,我们把点G称为基点(base point)。
现在我们描述一个利用椭圆曲线进行加密通信的过程:
1、用户A选定一条椭圆曲线Ep(a,b),并取椭圆曲线上一点,作为基点G。
2、用户A选择一个私有密钥k,并生成公开密钥K=kG。
3、用户A将Ep(a,b)和点K,G传给用户B。
4、用户B接到信息后 ,将待传输的明文编码到Ep(a,b)上一点M(编码方法很多,这里不作讨论),并产生一个随机整数r。
5、用户B计算点C1=M+rK;C2=rG。
6、用户B将C1、C2传给用户A。
7、用户A接到信息后,计算C1-kC2,结果就是点M。因为 C1-kC2=M+rK-k(rG)=M+rK-r(kG)=M
再对点M进行解码就可以得到明文。
在这个加密通信中,如果有一个偷窥者H ,他只能看到Ep(a,b)、K、G、C1、C2,而通过K、G 求k 或通过C2、G求r 都是相对困难的,因此,H无法得到A、B间传送的明文信息。
ElGamal加密算法
算法定义
ELGamal密码体制是T.ElGamal在1985年提出的公钥密码体制。它的安全性是基于求解离散对数问题的困难性,是RSA以后比较有希望的一个公钥密码。美国的DSS(Digital Signature Standard)的DSA(Digital Signature Algorithm)算法就是经ElGamal算法演变而来。目前DSA算法应用也非常广泛。
数学难题
1、有两个全局公开的参数,一个素数q和一个整数a,a是q的一个原根。
2、假设用户A和B希望交换一个密钥,用户A选择一个作为私有密钥的随机数XA<q,并计算公开密钥YA=a^XA mod q。A对XA的值保密存放而使YA能被B公开获得。类似地,用户B选择一个私有的随机数XB<q,并计算公开密钥YB=a^XB mod q。B对XB的值保密存放而使YB能被A公开获得。
3、用户A产生共享秘密密钥的计算方式是K = (YB)^XA mod q。同样,用户B产生共享秘密密钥的计算是K = (YA)^XB mod q。这两个计算产生相同的结果:
K = (YB)^XA mod q
= (a^XB mod q)^XA mod q
= (a^XB)^XA mod q (根据取模运算规则得到)
= a^XBXA mod q
= (a^XA)^XB mod q
= (a^XA mod q)^XB mod q
= (YA)^XB mod q
因此相当于双方已经交换了一个相同的秘密密钥。
4、因为XA和XB是保密的,一个敌对方可以利用的参数只有q、a、YA和YB。因而敌对方被迫取离散对数来确定密钥。例如,要获取用户B的秘密密钥,敌对方必须先计算
XB = inda ,q(YB)
然后再使用用户B采用的同样方法计算其秘密密钥K。
Diffie-Hellman密钥交换算法的安全性依赖于这样一个事实:虽然计算以一个素数为模的指
本文使用 CC BY-NC-SA 3.0 中国大陆 协议许可
具体请参见 知识共享协议
本文链接:https://zyhang8.github.io/2019/09/27/cipher-exp3/
