c++

Author Avatar
Euan 9月 01, 2019
  • 在其它设备中阅读本文章

C++算法分类

KxZS5F.jpg

哲学

  • 迭代为人，递归为神

基本语法

命名

  • 类的名称都要以大写字母“C”开头，后跟一个或多个单词。为便于界定，每个单词的首字母要大写
  • 函数名应当使用”动词”或者”动词＋名词”（动宾词组）的形式。例如：”GetName()”, “SetValue()”, “Erase()”, “Reserve()” ….
  • 函数的名称由一个或多个单词组成。为便于界定，每个单词的首字母要大写。
  • 保护成员函数的开头应当加上一个下划线“_”以示区别，例如：”_SetState()”
  • 类似地，私有成员函数的开头应当加上两个下划线“”，例如：”DestroyImp()”
  • 回调和事件处理函数习惯以单词“On”开头。例如：”_OnTimer()”, “OnExit()”
  • 虚函数习惯以“Do”开头，如：”DoRefresh()”, “_DoEncryption()”
前缀 说明
无 局部变量
m_ 类的成员变量（member）
sm_ 类的静态成员变量（static member）
s_ 静态变量（static）
g_ 外部全局变量（global）
sg_ 静态全局变量（static global）
gg_ 进程间共享的共享数据段全局变量（global global）

数据类型

  • int 类型，4Bytes 32位，最小-2147483648 最大 2147483647
  • PI=atan(1.0)*4
  • sizeof返回的必定是无符号整形,在标准c中通过 typedef 将返回值类型定义为size_t.若用printf输出size_t类型时,C99中定义格式符%zd;若编译器不支持可以尝试%u或%lu.sizeof，获取操作数占用的内存空间字节数,返回类型size_t；strlen，获取字符数组实际使用的字节数,不包含数组结尾符’\0’，返回类型size_t

ASCII、unicode与Utf8之间的相互转化

常用的Ascii：空格的ASCII码值为32；数字0到9的ASCII码值分别为48到57；大写字母“A”到“Z”的ASCII码值分别为65到90；小写字母“a”到“z”的ASCII码值分别为97到到122

16进制余数大于10加55

ASCII、unicode与Utf8之间的相互转化

wstring和string区别

wstring的存在主要是因为有汉字，差异就在char还是wchar_t

所以wchar_t本质上是一个unsigned short，2个字节的大小，即16bit

  • 窄字符，一般用于满足ASCII编码，一个单元一个char
  • 宽字符，一般用于满足UNICODE编码，一个单元两个char

也就是说，宽字符，每表示一个字符其实是占了16bit，即2个char的大小。而汉字就是需要16bit来表示。

1
2
3
4
5
6
string s = "你好！";
cout << s[2] << s[3] << endl;

wcout.imbue(std::locale("chs"));
wstring ws = L"你好！";
wcout << ws[1] << endl;

vector

遍历容器

1
2
3
4
for (int i : p)
    {
        cout << i;
    }
  • vector a ; //声明一个int型向量a
  • vector a(10) ; //声明一个初始大小为10的向量
  • vector a(10, 1) ; //声明一个初始大小为10且初始值都为1的向量
  • vector b(a) ; //声明并用向量a初始化向量b
  • vector b(a.begin(), a.begin()+3) ; //将a向量中从第0个到第2个(共3个)作为向量b的初始值
  • int n[] = {1, 2, 3, 4, 5} ;
  • vector a(n, n+5) ; //将数组n的前5个元素作为向量a的初值
  • vector a(&n[1], &n[4]) ; //将n[1] - n[4]范围内的元素作为向量a的初值
  • c.back() // 传回最后一个数据，不检查这个数据是否存在。
  • c.begin() // 传回迭代器中的第一个数据地址。
  • c.capacity() // 返回容器中数据个数。
  • c.clear() // 移除容器中所有数据。
  • c.empty() // 判断容器是否为空。
  • c.end() // 指向迭代器中末端元素的下一个，指向一个不存在元素。
  • c.erase(pos) // 删除pos位置的数据，传回下一个数据的位置。
  • c.erase(beg,end) //删除[beg,end)区间的数据，传回下一个数据的位置。
  • c.front() // 传回第一个数据。
    c.insert(pos,elem) // 在pos位置插入一个elem拷贝，传回新数据位置。
    c.insert(pos,n,elem) // 在pos位置插入n个elem数据。无返回值。
    c.insert(pos,beg,end) // 在pos位置插入在[beg,end)区间的数据。无返回值。
  • c.max_size() // 返回容器中最大数据的数量。
  • c.pop_back() // 删除最后一个数据。
  • c.push_back(elem) // 在尾部加入一个数据。
  • c.rbegin() // 传回一个逆向队列的第一个数据。
  • c.rend() // 传回一个逆向队列的最后一个数据的下一个位置。
  • c.resize(num) // 重新指定队列的长度。
  • c.reserve() // 保留适当的容量。
  • c.size() // 返回容器中实际数据的个数。
  • c1.swap(c2)
  • swap(c1,c2) // 将c1和c2元素互换。同上操作。
  • *max_element() //最大值
  • vector::iterator iter //迭代器
  • accumulate(va.begin(),va.end(),0); // 求和
  • size_type //size_type 就是这个 size 值的类型，你只要声明一个 size_type 类型的变量就能存下“元素个数”的值

vector常用函数

转换说明符

  • %a(%A) 浮点数、十六进制数字和p-(P-)记数法(C99)
  • %d 有符号十进制整数
  • %e(%E) 浮点数指数输出[e-(E-)记数法]
  • %g(%G) 浮点数不显无意义的零”0”
  • %i 有符号十进制整数(与%d相同)
  • %u 无符号十进制整数
  • %o 八进制整数 e.g. 0123
  • %x(%X) 十六进制整数0f(0F) e.g. 0x1234
  • %p 指针
  • %% “%”
  • 左对齐：”-“ e.g. “%-20s”
  • 右对齐：”+” e.g. “%+20s”/“%20s”
  • “%m.ns”：输出m位，取字符串(左起)n位，左补空格 e.g. “%7.2s” 输入CHINA 输出” CH”

常用头函数

1
2
3
4
#include <iomanip> //流操作符
#include <iostream>
#include <string.h>
#include <math.h>

运算符

左移右移运算符

0正1负

int i = 0x40000000; //16进制的40000000,为2进制的01000000…0000

i = i << 1;

i在左移1位之后就会变成0x80000000,也就是2进制的100000…0000,符号位被置1,其他位全是0,变成了int类型所能表 示的最小值,32位的int这个值是-2147483648,溢出

左移里一个比较特殊的情况是当左移的位数超过该数值类型的最大位数时,编译器会用左移的位数去模类型的最大位数,然后按余数进行移位,如:

int i = 1, j = 0x80000000; //设int为32位

i = i << 33; // 33 % 32 = 1 左移1位,i变成2

j = j << 33; // 33 % 32 = 1 左移1位,j变成0,最高位被丢弃

左移1位相当于乘以2,那么左移n位就是乘以2的n次方了

左移就是: 丢弃最高位,0补最低位

符号位向右移动后,正数的话补0,负数补1

同样当移动的位数超过类型的长度时,会取余数,然后移动余数个位.

函数

cin,getline,get

  • cin>> == cin.operator>>()
  • 若缓冲区中第一个字符是空格、tab或换行这些分隔符时，cin>>会将其忽略并清除，继续读取下一个字符，若缓冲区为空，则继续等待。但是如果读取成功，字符后面的分隔符是残留在缓冲区的，cin>>不做处理
  • 不想略过空白字符，那就使用 noskipws 流控制。比如cin>>noskipws>>input
  • istream类重载了get（)方法，分别为get（void）， get(char &, int)， get(char & , int , char)
  • getline()读取数据时，并非像cin>>那样忽略第一个换行符，getline()发现cin的缓冲区中有一个残留的换行符，不阻塞请求键盘输入，直接读取
  • get(char &, int) 第一个参数用于保存输入字符，第二个参数表示最大输入字符个数，存储个数往往比第二个参数小一
  • get（）会将换行符保留在输入序列中，这就导致了二次输入操作时，换行符会直接被读取，输入流会认为输入已经结束.如何解决:cin.get(ch1,20).get()
  • getline（）不是类方法。它将cin作为参数，指出到哪里去查找输入
  • cin.sync()来清空输入缓冲区；在流中fail()状态值无效的情况下，执行cin.sync(); 清空流是无效的
  • cin.clear(); // 将流中的所有状态值都重设为有效值
  • cin.fail() //输入错误 ，为1
  • cin.sync() 可不一定能清空缓冲区，具体实现跟编译器相关，所以不具备很好的移植性，慎用;vscode 使用cin.ignore(std::numeric_limitsstd::streamsize::max(), ‘\n’); 代替cin.sync()

setw(int n)

用来控制输出间隔

1
2
3
4
5
cout<< setw(4) <<123 <<1234<<endl;
cout << 1 <<setw(7) << 1234 << endl;
cout << 1 << setw(7) << 1234567891234 << endl;
cout << 1 << 1234 << setw(7) << endl;
cout<<setfill('*')<<setw(5)<<'a'<<endl;
1
2
3
4
5
6
7
8
9
 1231234

1   1234

11234567891234

11234

****a

四舍五入

  • ceil(x)返回不小于x的最小整数值（然后转换为double型）
  • floor(x)返回不大于x的最大整数值
  • round(x)返回x的四舍五入整数值

log\exp

自定义以m为底，求log n的值,需要double a=log(n)/log(m)

exp（n）值为e^n次方

基本算法

遍历

1+2+3+n:(n+1) * n / 2;

枚举

贪心

递归和分治

递推

构造

模拟

搜索

深度优先搜索

广度优先搜索

双向搜索

启发式搜索

记忆化搜索

计算几何

几何公式

叉积和点积的运用

多边形的简单算法

凸包

扫描线算法

多边形的内核

几何工具的综合应用

半平面求交

可视图的建立

点集最小圆覆盖

对踵点

数学

组合数学

排列组合

递推关系

容斥原理

抽屉原理

置换群与Polya定理

母函数

MoBius反演

偏序关系理论

数论

进制位

同余模运算

高斯消元

概率问题

扩展欧几里德

博弈论

极大极小过程

Nim过程

图论

拓扑排序

最小生成树

最短路

二分图

匈牙利算法

KM算法

网络流

最小费用最大流

最小割模型、网络流规约

差分约束系统建立和求解

双连通分量

强连通分支及其缩点

图的割边与割点

动态规划

背包问题

01背包

完全背包

多维背包

多里背包

基本DP

区间DP

环形DP

判定行DP

棋盘分割

最长公共子序列

最长上升子序列

二分判定型DP

树形动态规划

最大独立集

状态压缩DP

哈密顿路径问题

四边形不等式理论

单调队列优化

数据结构

串

KMP

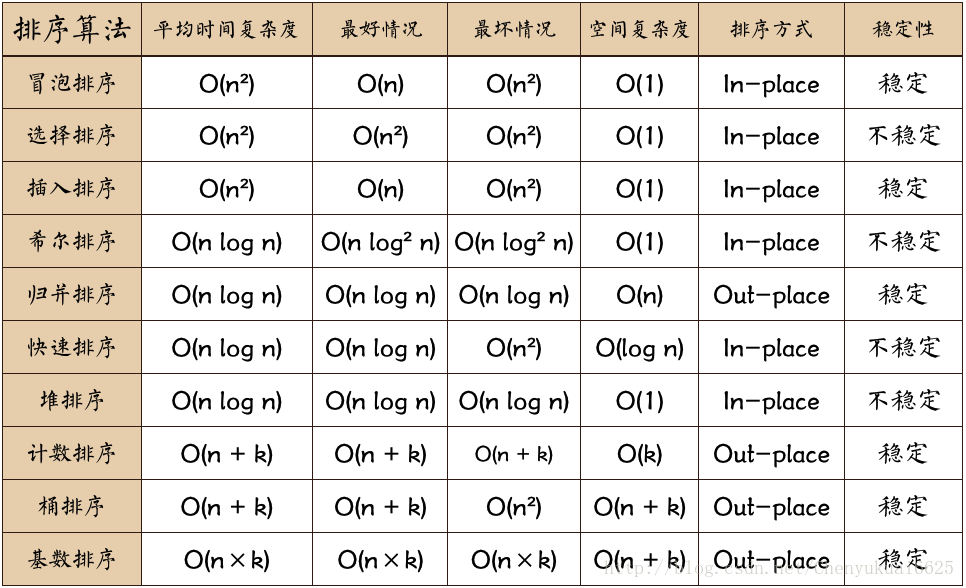
排序

paixu_1

  • 稳定：如果a原本在b前面，而a=b，排序之后a仍然在b的前面。
  • 不稳定：如果a原本在b的前面，而a=b，排序之后 a 可能会出现在 b 的后面。
  • 时间复杂度：对排序数据的总的操作次数。反映当n变化时，操作次数呈现什么规律。
  • 空间复杂度：是指算法在计算机内执行时所需存储空间的度量，它也是数据规模n的函数。

比较类排序

交换排序
冒泡排序

时间复杂度：O(N2) 　　稳定性：稳定

快速排序/划分交换排序

时间复杂度：O(NlogN) 　　稳定性：不稳定

枢值/基准数，哨兵

插入排序
简答插入排序

时间复杂度：O(N2) 　　稳定性：稳定

希尔排序

时间复杂度：通常认为是O(N3/2) ，未验证　　稳定性：不稳定

选择排序
简单选择排序

时间复杂度：O(N2) 　　稳定性：不稳定

堆排序

时间复杂度：O(NlogN) 　　稳定性：不稳定

堆积树（堆）。堆分为大根堆和小根堆，是完全二叉树。

归并排序
简单归并排序

时间复杂度：O(NlogN) 　　稳定性：稳定

分治

多路归并排序

非比较排序

基数排序

时间复杂度：O(x*N) 　　稳定性：稳定

  • LSD从低位开始排到高位，每排一位都是把各个桶合并，再按下一位排序；
  • MSD从高位开始排到低位，排完一位后不合并桶，相同的高位划分子桶继续分配，最后再合并
桶排序
计数排序

哈希表

二分

并查集

霍夫曼树

堆

线段树

二叉树

  • 完全二叉树： 除了最后一层之外的其他每一层都被完全填充，并且所有结点都保持向左对齐。
  • 满二叉树：除了叶子结点之外的每一个结点都有两个孩子，每一层(当然包含最后一层)都被完全填充。
  • 完满二叉树：除了叶子结点之外的每一个结点都有两个孩子结点。

树的树状数组

RMQ

本文使用 CC BY-NC-SA 3.0 中国大陆 协议许可
具体请参见 知识共享协议
本文链接：https://zyhang8.github.io/2019/09/01/c++/